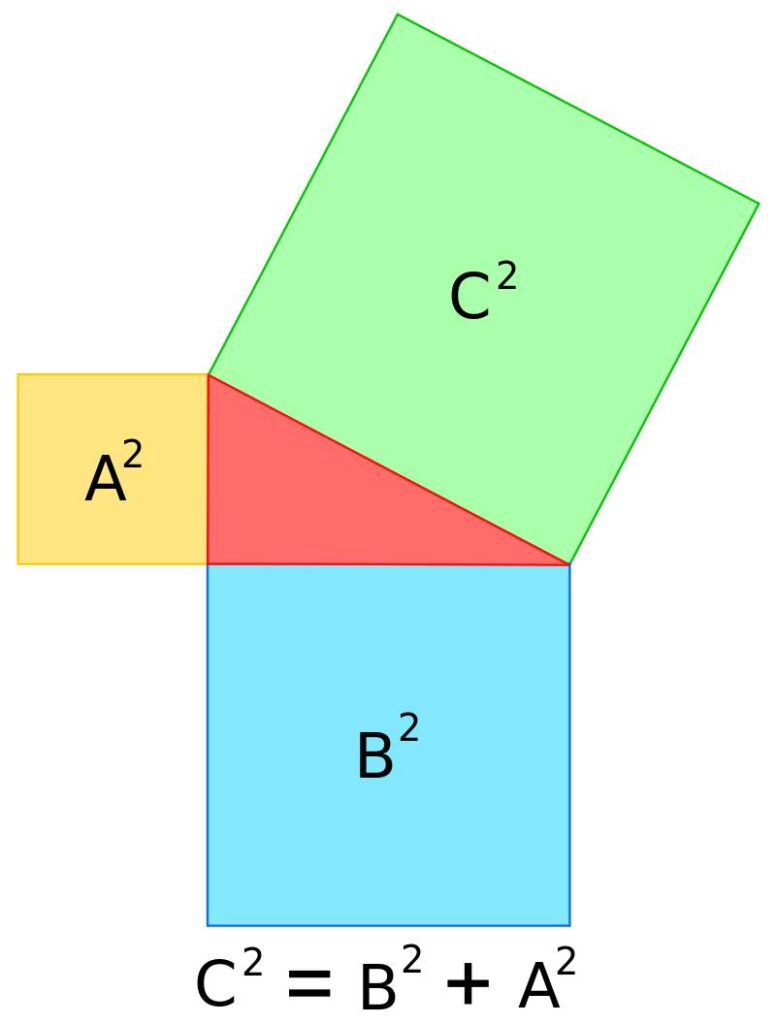
Le terne pitagoriche hanno un sacco di caratteristiche.

A- Solo uno dei cateti è pari, l’altro è dispari e l'ipotenusa è sempre dispari.

B- I due cateti sono coprimi (primi fra di loro).

C- Uno dei cateti è sempre divisibile per 3 (deriva dalla terna 3-4-5).

D- Uno dei cateti è sempre divisibile per 4 (deriva dalla terna 3-4-5).

E- Il prodotto dei due cateti è sempre divisibile per 12 (ovvio dalla C e dalla D).

F- Uno dei lati è sempre divisibile per 5 (deriva dalla terna 3-4-5).

G- Il prodotto dei tre lati è sempre divisibile per 60 (ovvio dalla E e dalla F).

H- Due terne pitagoriche posso essere combinate per generarne una terza.

I- Esistono infinite terne pitagoriche dove l'ipotenusa è uguale al maggiore dei cateti +1.

J- Esistono infinite terne pitagoriche dove l'ipotenusa è uguale al maggiore dei cateti +2.

K- Esistono infinite terne pitagoriche dove i cateti differiscono di 1.

L- Esistono coppie di terne pitagoriche con differente ipotenusa e stessa area.

M- Esistono coppie di terne pitagoriche con differenti cateti e stessa ipotenusa.

N- Esistono coppie di terne pitagoriche con lo stesso cateto.

O- Nelle terne pitagoriche primitive, l'ipotenusa non è mai un multiplo di 3.

P- Numeri primi esprimibili come (4n + 1) in rapporto alle terne pitagoriche.

Le prime due regole sono già state dimostrate in un post precedente.

C- Per dimostrare che uno dei cateti è sempre divisibile per 3, usiamo il primo dei sistemi di equazioni che ho indicato in precedenza, quello per k dispari.

a = k

b = (k^2 - 1)/ 2

Se k è divisibile per 3, a è divisibile per 3.

Se k non è divisibile per 3, può avere solo una forma del tipo (x+1) o (x+2), dove x è un numero divisibile per 3 (x=3w). Applichiamo (x+1) al cateto b.

b = (x+1)^2 - 1)/ 2 = (x^2+2x+1-1)/2 = (x^2+2x)/2 = (3w)^2+6w = 9w^2+6w = 3(3w^2+2w)

Abbiamo dimostrato che b è divisibile per 3, qualsiasi valore abbia w.

Applichiamo (x+2) al cateto b.

b = (x+2)^2 - 1)/ 2 = (x^2+4x+4-1)/2 = (x^2+4x+3)/2 = [(3w)^2+12w+3]/2 = (9w^2+12w+3)/2 = 3(3w^2+4w+1)/2

Abbiamo dimostrato che b è divisibile per 3, qualsiasi valore abbia w.

Ora usiamo il secondo dei sistemi di equazioni che ho indicato, quello per k pari.

a = 2*k

b = k^2 -1

Se k è divisibile per 3, a è divisibile per 3.

Se k non è divisibile per 3, può avere solo una forma del tipo (x+1) o (x+2), dove x è un numero divisibile per 3 (x=3w). Applichiamo (x+1) al cateto b.

b = (x+1)^2 - 1 = (x^2+2x+1-1) = (x^2+2x) = (3w)^2+6w = 9w^2+6w = 3(3w^2+2w)

Abbiamo dimostrato che b è divisibile per 3, qualsiasi valore abbia w.

Applichiamo (x+2) al cateto b.

b = (x+2)^2 - 1) = (x^2+4x+4-1) = (x^2+4x+3) = [(3w)^2+12w+3] = (9w^2+12w+3) = 3(3w^2+4w+1)

Abbiamo dimostrato che b è divisibile per 3, qualsiasi valore abbia w.

Abbiamo dimostrato che, scegliendo un valore qualsiasi di k, generiamo sempre una terna pitagorica dove uno dei cateti è multiplo di 3.

D- Per dimostrare che uno dei cateti è sempre divisibile per 4, usiamo il primo dei sistemi di equazioni suddetti.

a = k

b = (k^2 - 1)/ 2

Se k è divisibile per 4, a è divisibile per 4.

Se k non è divisibile per 4, può avere solo una forma del tipo (x+1) o (x+2) o (x+3) dove x è un numero divisibile per 4 (4w). Tuttavia, questo insieme di equazioni vale per k dispari, ma (x+2), con x divisibile per 4, è pari e quindi per quel caso dobbiamo usare il secondo sistema. Applichiamo (x+1) al cateto b.

b = (x+1)^2 - 1)/ 2 = (x^2+2x+1-1)/2 = (x^2+2x)/2 = (4w)^2+8w = 16w^2+8w = 4(4w^2+2w)

Abbiamo dimostrato che b è divisibile per 4, qualsiasi valore abbia w.

Applichiamo (x+3) al cateto b.

b = (x+3)^2 - 1)/ 2 = (x^2+6x+9-1)/2 = (x^2+6x+8)/2 = (16w^2+24w+8)/2 = 8w^2+12w+4 = 4(2w^2+3w+1)

Abbiamo dimostrato che b è divisibile per 4, qualsiasi valore abbia w.

Ora usiamo il secondo sistema per il caso (x+2).

a = 2*k = 2*(x+2) = 2x+4 = 8w+4 = 4(2w+1)

Abbiamo dimostrato che a è divisibile per 4, qualsiasi valore abbia w.

Abbiamo dimostrato che, scegliendo un valore qualsiasi di k, generiamo sempre una terna pitagorica dove uno dei cateti è multiplo di 4. Abbiamo quindi dimostrato che il prodotto dei cateti è sempre divisibile per 12.

F- Per dimostrare che uno dei lati è sempre divisibile per 5, usiamo i due sistemi di equazioni.

K DISPARI

a = k

b = (k^2 - 1)/ 2

c = (k^2 + 1)/ 2

Se k è divisibile per 5, a è divisibile per 5.

Se non lo è, può avere solo una forma del tipo (x+2) o (x+4) dove x è un numero divisibile per 5 (5w).

K PARI

a = 2*k

b = k^2 -1

c = k^2 +1

Se k è divisibile per 5, a è divisibile per 5.

Se non lo è, può avere solo una forma del tipo (x+1) o (x+3) dove x è un numero divisibile per 5 (5w).

Applichiamo il caso (x+2) al primo sistema.

b = ((x+2)^2 - 1)/ 2 = (x^2+4x+4-1)/2 = (x^2+4x+3)/2 = [(5w)^2+20w+3]/2 = 25w^2+20w+3 (non è detto sia divisibile per 5).

c = ((x+2)^2 + 1)/ 2 = (x^2+4x+4+1)/2 = (x^2+4x+5)/2 = [(5w)^2+20w+5]/2 = 25w^2+20w+5 = 5(5w^2+4w+1).

L'ipotenusa è divisibile per 5 qualsiasi valore abbia w.

Applichiamo il caso (x+4) al primo sistema.

b = ((x+4)^2 - 1)/ 2 = (x^2+8x+16-1)/2 = (x^2+8x+15)/2 = [(5w)^2+40w+15]/2 = (25w^2+40w+15)/2 = 5(5w^2+8w+3)/2.

c = ((x+4)^2 + 1)/ 2 = (x^2+8x+16+1)/2 = (x^2+8x+17)/2 = [(5w)^2+40w+17]/2 = (25w^2+40w+17)/2 (non è detto sia divisibile per 5).

Il cateto b è divisibile per 5 qualsiasi valore abbia w.

Applichiamo il caso (x+1) al secondo sistema.

b = k^2 -1 = (x+1)^2 -1 = x^2-2x+1-1 = x^2-2x = (5w)^2-10w = 25w^2-10w = 5(5w^2-2w).

c = k^2 +1 = (x+1)^2 +1 = x^2-2x+1+1 = x^2-2x+2 = (5w)^2-10w+2 = 25w^2-10w+2 (non è detto sia divisibile per 5).

Il cateto b è divisibile per 5 qualsiasi valore abbia w.

Applichiamo il caso (x+3) al secondo sistema.

b = k^2 -1 = (x+3)^2 -1 = x^2-6x+9-1 = x^2-6x+8 = (5w)^2-30w+8 = 25w^2-30w+8 (non è detto sia divisibile per 5).

c = k^2 +1 = (x+3)^2 +1 = x^2-6x+9+1 = x^2-6x+10= (5w)^2-30w+10= 25w^2-30w+10= 5(5w^2-6w+2).

L'ipotenusa è divisibile per 5 qualsiasi valore abbia w.

Abbiamo dimostrato che, scegliendo un valore qualsiasi di k, generiamo sempre una terna pitagorica dove uno dei lati è multiplo di 5. Abbiamo anche dimostrato che il prodotto dei lati è sempre divisibile per 60.

H- Due terne pitagoriche posso essere combinate per generarne una terza.

Se indichiamo le due terne in questo modo:

a^2 + b^2 = c^2

x^2 + y^2 = z^2

la formula da usare sarà questa:

(ax - by)^2 + (ay + bx)^2 = (cz)^2

Ecco un esempio.

(a, b, c) = (3, 4, 5)

(x, y, z) = (5, 12, 13)

(3*5 - 4*12)^2 + (3*12 + 4*5)^2 = (5*13)^2

(15 - 48)^2 + (36 + 20)^2 = 65^2

(- 33)^2 + 56^2 = 65^2

1089 + 3136 = 4225

I- Esistono infinite terne pitagoriche dove l'ipotenusa è uguale al maggiore dei cateti +1 e si dimostra usando le formule di Euclide.

c - b = 1

m^2 + n^2 - 2mn = 1

(m - n)^2 = 1

m - n = 1

m = n + 1

Sostituendo m con (n+1) nelle formule di Euclide, si trovano tutte le terne dove l'ipotenusa è uguale al maggiore dei cateti +1

b = 2n(n+1) = 2n^2+2n

c = (n+1)^2 + n^2 = 2n^2+2n+1 = b+1

J- Esistono infinite terne pitagoriche dove l'ipotenusa è uguale al maggiore dei cateti +2 e si dimostra usando le formule di Euclide e ponendo n=1.

Più in generale, ci sono infinite terne pitagoriche dove l'ipotenusa è uguale al maggiore dei cateti +2k^2 e si trovano ponendo n = k nelle formule di Euclide.

K- Esistono infinite terne pitagoriche dove i cateti differiscono di 1.

Per esempio: 20^2 + 21^2 = 29^2.

L- Esistono coppie di terne pitagoriche con differente ipotenusa e stessa area.

Per esempio, i due triangoli 20-21-29 e 12-35-37 danno entrambi come area 210.

Oppure i due triangoli 60-91-109 e 28-195-197 danno entrambi come area 2730.

M- Esistono coppie di terne pitagoriche con differenti cateti e stessa ipotenusa.

Per esempio, i due triangoli 13-84-85 e 36-77-85.

Oppure i due triangoli 17-144-145 e 24-143-145.

N- Esistono coppie di terne pitagoriche con lo stesso cateto.

Per esempio, i due triangoli 20-21-29 e 20-99-101.

Oppure i due triangoli 60-91-109 e 60-221-229.

O- Nelle terne pitagoriche primitive, l'ipotenusa non è mai un multiplo di 3.

Questa dimostrazione mi manca, chi la possiede la scriva nei commenti, grazie.

P- Se un numero primo P è esprimibile nella forma (4n + 1), allora ha queste proprietà:

(per n=1 si ottiene 5)

1) P è la somma di due quadrati (5 = 4 + 1).

2) P è l'ipotenusa di 1 terna pitagorica (5-4-3).

3) P^2 è l'ipotenusa di 2 terne pitagoriche (25-20-15 e 25-24-7).

4) P^3 è l'ipotenusa di 3 terne pitagoriche (125-100-75 e 125-120-35 e 125-117-44).

(per n=3 si ottiene 13)

1) P è la somma di due quadrati (13 = 9 + 4).

2) P è l'ipotenusa di 1 terna pitagorica (13-12-5).

3) P^2 è l'ipotenusa di 2 terne pitagoriche (169-156-65 e 169-120-119).

4) P^3 è l'ipotenusa di 3 terne pitagoriche (2197-2028-845 e 2197-1560-1547 e 2197-?-?).