Coπrimalità: Presi due numeri naturali maggiori di 1
qual è la probabilità che essi siano coprimi, ovvero che il loro massimo comun divisore sia 1?
La risposta è sorprendente: la probabilità è p=1/ζ(2)=6/π²≃60,8%.
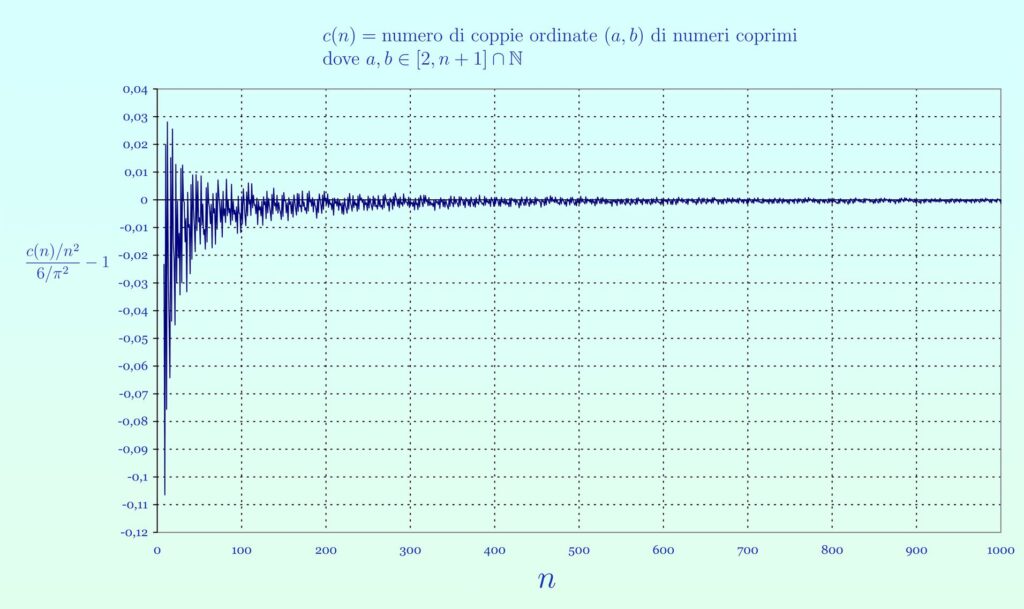
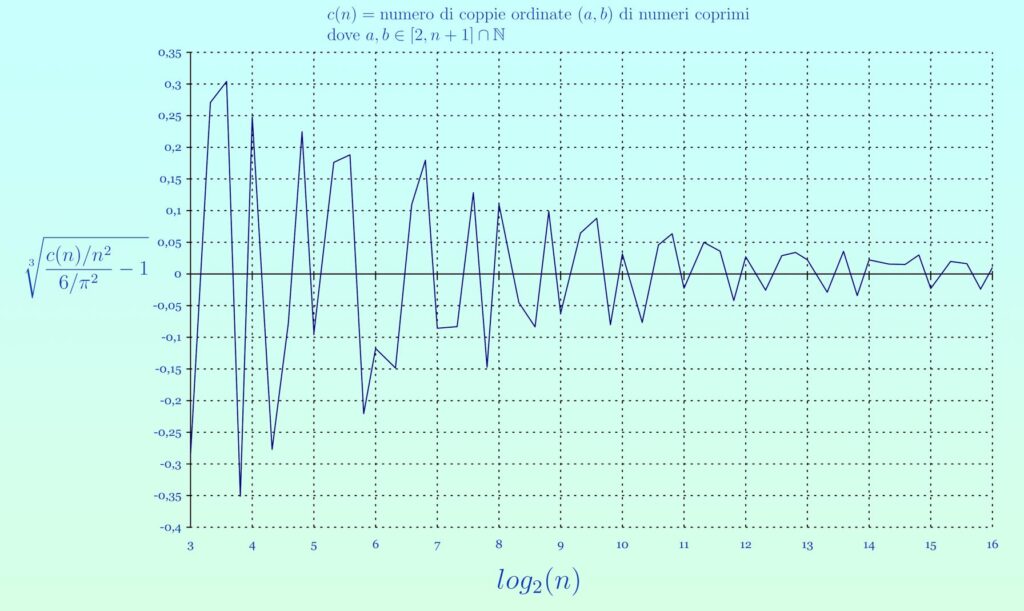
Ho provato a “verificare sul campo” questo valore, considerando n numeri da 2 a n+1 e contando quante sono le coppie ordinate (a,b) di numeri coprimi, con 2 ≤ a,b ≤n+1. Chiamo c(n) il numero di queste coppie. Il rapporto c(n)/n² dovrebbe convergere a 6/π² al tendere di n a infinito. Le immagini allegate testimoniano che questo in effetti accade. Nel secondo grafico, quello con scala delle ascisse logaritmica, nelle ordinate ho preso la radice cubica per non far appiattire in modo illeggibile il grafico. Tenete quindi presente che, ad esempio, a 0,05 corrisponde un valore di 0,000125. Per n=65536 il rapporto fra c(n)/n² e 6/π² differisce da 1 per circa 10⁻⁶
Così però ho fatto un “esperimento”, ancorché esaustivo, con numeri “piccoli”, minori o uguali a 65537. Ho allora fatto anche un test Montecarlo, prendendo per 100 volte 2²⁴ (circa 17 milioni) coppie di numeri generati casualmente, compresi fra 2 e 2⁶⁴+1 (numero grandicello, pari circa a 18 miliardi di miliardi) e ho contato il rapporto fra coppie di numeri coprimi e numero totale di coppie. Il risultato, riportato in termini di media e deviazione standard è stato
r=(0,999996±0,000177)∙6/π²
Ancora Montecarlo, prendendo per 100 volte 2²⁴ coppie di numeri generati casualmente, compresi fra 2 e 2⁹⁶+1 (circa 79 miliardi di miliardi di miliardi)
r=(1,000015±0,000188)∙6/π²
In entrambi i casi la deviazione standard attesa è 0,000175 mentre l’errore atteso sulla media è 0,000017.