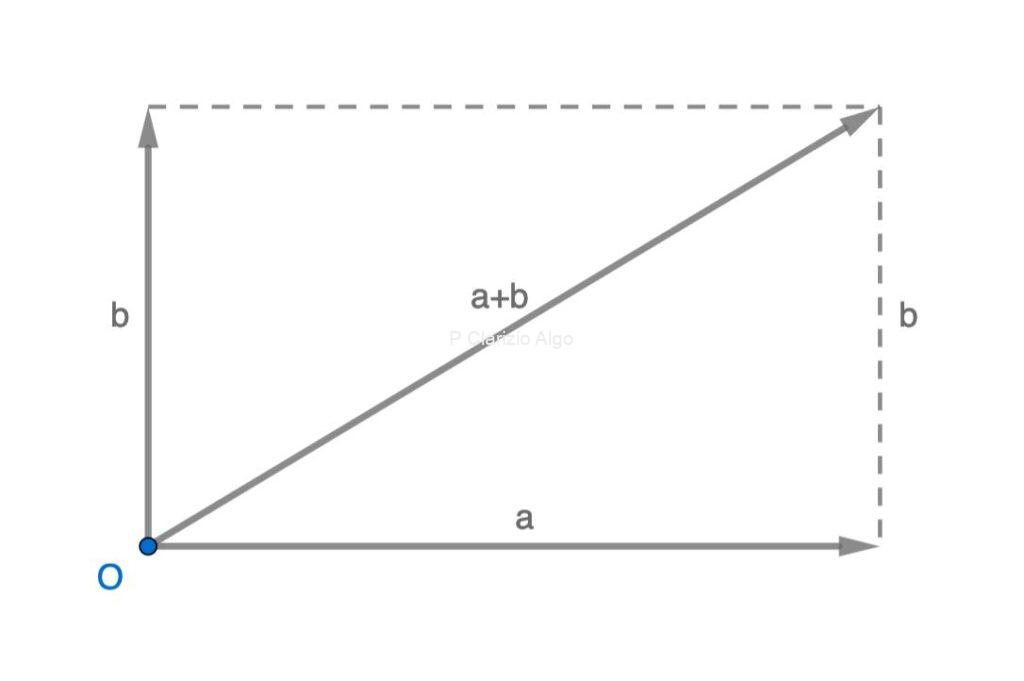
dimostrazione "immediata" del teorema di Pitagora, basata sul calcolo vettoriale
Se si conosce un po' di calcolo vettoriale, il procedimento è in effetti molto semplice. La lunghezza di un vettore x (o, in gergo, "norma", o modulo) è infatti data da ‖x‖ = √(x·x), dove "·" indica il prodotto scalare tra vettori (attenzione, non la moltiplicazione tra numeri).
Presi due vettori perpendicolari di lunghezza a e b (i cateti), l'ipotenusa ha la stessa lunghezza c del vettore somma a+b (che si può rappresentare con la regola del parallelogrammo). Inoltre, essendo i cateti perpendicolari, il loro prodotto scalare è nullo: a·b = b·a = 0.
Sfruttando la (bi)linearità e la simmetria del prodotto scalare, abbiamo:
‖c‖² =
= ‖a+b‖² =
= (a+b)·(a+b) =
= a·a + b·b + a·b + b·a =
= ‖a‖² + ‖b‖² + 2a·b =
= ‖a‖² + ‖b‖².
(I più smaliziati ritroveranno in questo calcolo anche il teorema dei coseni che vale per triangoli qualsiasi; in quel caso a·b = ‖a‖ × ‖b‖ × cos(𝜗), dove 𝜗, in generale diverso da 90°, è l’angolo compreso tra i lati a e b).
======================================
Questa dimostrazione a me piace però vederla al contrario, cioè come la motivazione che porta a definire il concetto di ortogonalità tra vettori in relazione al loro prodotto scalare. Infatti un triangolo è rettangolo se e solo se i suoi lati rispettano il teorema di Pitagora. Ma dall'uguaglianza sopra vediamo che ‖c‖² = ‖a‖² + ‖b‖² se e solo se a·b = 0. Il triangolo è rettangolo (cioè a e b sono perpendicolari) se e solo se a·b = 0.
Questa è la motivazione che spinge a definire due vettori come ortogonali se hanno prodotto scalare nullo. Questo concetto si estende in algebra e in analisi: si definiscono prodotti scalari molto più complicati e astratti, mantenendo questa definizione fondamentale del concetto di ortogonalità.
Tanto per fare un esempio complicato, l'analisi di Fourier negli spazi di Hilbert utilizza questo concetto: le funzioni eⁱᵏᵗ sono una base di vettori ortogonali nello spazio di funzioni (eⁱᵏᵗ · eⁱᵐᵗ = 0 se k ≠ m, dove · è un opportuno prodotto scalare tra "vettori" in questo spazio di funzioni).
Al di là dei dettagli e delle complicazioni, mi piace pensare come questi concetti relativamente avanzati hanno le loro fondamenta su un risultato così semplice come il teorema di Pitagora.