Per calcolare π il noto siceliota Archimede: Machinazione per spaccare il caπello in 4
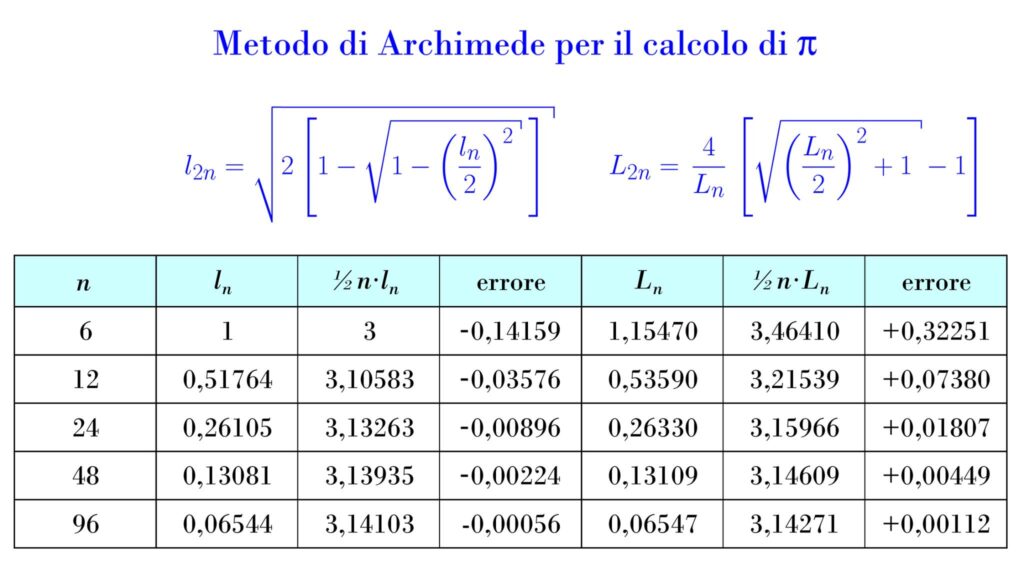
utilizzò come valori limitanti il semiperimetro dei poligoni regolari inscritti in una circonferenza di raggio unitario e quello dei poligoni regolari circoscritti alla stessa circonferenza. In particolare, conoscendo lₙ, lato del poligono inscritto con n lati, è possibile ricavare l₂ₙ e analogamente conoscendo Lₙ, lato del poligono circoscritto con n lati, è possibile ricavare L₂ₙ (vedi prima immagine). Si parte da l₆=1 e L₆=2/√3.
Questo metodo ha due grandi svantaggi: il primo è il dovere calcolare radici quadrate (avete mai sperimentato l’ebbrezza di calcolare una radice quadrata con carta e penna? e tenete conto che noi abbiamo il sistema decimale, i Greci non l’avevano) e il secondo è la lentissima convergenza: ad ogni raddoppio dei lati l’errore diminuisce solo di un fattore circa uguale a 4. D’altronde, all’epoca non c’era altro, sicché Archimede si dovette accontentare. Con un poligono inscritto di 96 lati Archimede stabilì che π>3+10/71, e con un poligono circoscritto di altrettanti lati che π<3+1/7. In notazione decimale noi scriveremmo 3,1408<π<3,1428.
Archimede non poteva sapere che calcolando ⅙n(2lₙ+Lₙ) la convergenza è molto più rapida, ed infatti ⅙×96×(2l₉₆+L₉₆) differisce da π per meno di 2×10⁻⁷.
Questo metodo ha due grandi svantaggi: il primo è il dovere calcolare radici quadrate (avete mai sperimentato l’ebbrezza di calcolare una radice quadrata con carta e penna? e tenete conto che noi abbiamo il sistema decimale, i Greci non l’avevano) e il secondo è la lentissima convergenza: ad ogni raddoppio dei lati l’errore diminuisce solo di un fattore circa uguale a 4. D’altronde, all’epoca non c’era altro, sicché Archimede si dovette accontentare. Con un poligono inscritto di 96 lati Archimede stabilì che π>3+10/71, e con un poligono circoscritto di altrettanti lati che π<3+1/7. In notazione decimale noi scriveremmo 3,1408<π<3,1428.
Archimede non poteva sapere che calcolando ⅙n(2lₙ+Lₙ) la convergenza è molto più rapida, ed infatti ⅙×96×(2l₉₆+L₉₆) differisce da π per meno di 2×10⁻⁷.
La svolta arriva quasi 2000 anni dopo Archimede: nel 1671 James Gregory (1638-1675) scopre quella che noi oggi chiamiamo serie di Taylor per l’arcotangente:
arctan x=x-⅓x³+⅕x⁵-⅐x⁷… ,
serie scoperta poi indipendentemente da Leibniz (1646-1716) nel 1674. Il fatto che la serie abbia i termini a segni alterni risulta molto vantaggioso in quanto gli ultimi due valori della serie troncata forniscono un limite inferiore e superiore al valore della serie infinita, quindi c’è modo di stimare l’errore massimo commesso.
Poiché arctan(1)=π/4, questo suggerisce di trovare π calcolando 4(1-⅓+⅕-⅐…). Così però la serie converge molto lentamente, e per avere n decimali dobbiamo sommare 2×10ⁿ termini.
Arriva ora il nostro eroe, John Machin (1686-1751) (si pronuncia /'meɪtʃɪn/) che nel 1706 scopre (non sappiamo come) la formula
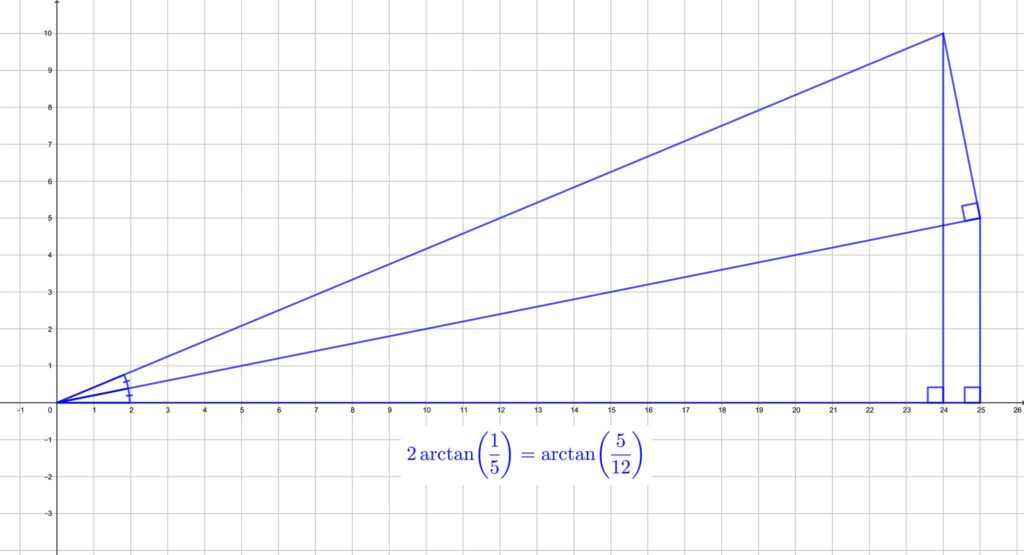
π/4=4 arctan(1/5)-arctan(1/239).
Utilizzando la serie di Gregory-Leibniz ora la convergenza è molto più rapida, e Machin riesce a calcolare π con ben 100 cifre decimali, e questo gli richiese il calcolo di una settantina di termini della serie relativa ad arctan(1/5) e di una quarantina di termini della serie relativa ad arctan(1/239). In suo onore, ogni espressione di π come somma o differenza di arcotangenti di frazioni viene chiamata Machin-like formula (in italiano potremmo tradurre con “formula di tipo Machin”). Possiamo dimostrare la formula di Machin utilizzando le formule di addizione e sottrazione per la tangente, oppure più elegantemente attraverso le identità complesse
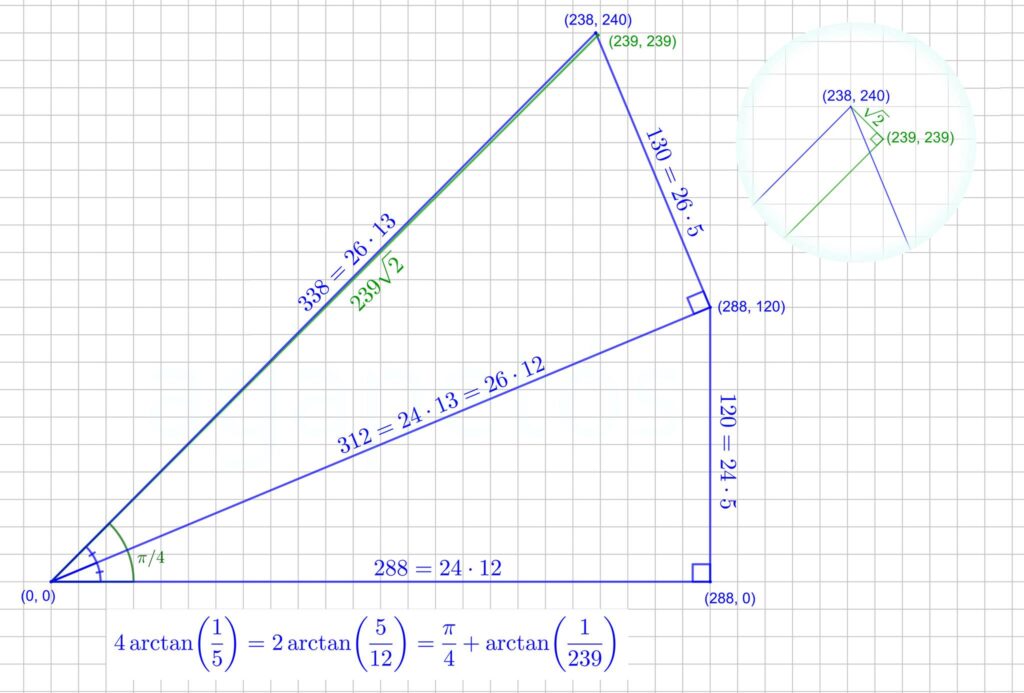
(5+i)⁴=(24+10i)²=476+480i=2(1+i)(239+i),
da cui 4 arg(5+i)=arg(1+i)+arg(239+i) ovvero
4 arctan(1/5)= π/4+arctan(1/239).
arctan x=x-⅓x³+⅕x⁵-⅐x⁷… ,
serie scoperta poi indipendentemente da Leibniz (1646-1716) nel 1674. Il fatto che la serie abbia i termini a segni alterni risulta molto vantaggioso in quanto gli ultimi due valori della serie troncata forniscono un limite inferiore e superiore al valore della serie infinita, quindi c’è modo di stimare l’errore massimo commesso.
Poiché arctan(1)=π/4, questo suggerisce di trovare π calcolando 4(1-⅓+⅕-⅐…). Così però la serie converge molto lentamente, e per avere n decimali dobbiamo sommare 2×10ⁿ termini.
Arriva ora il nostro eroe, John Machin (1686-1751) (si pronuncia /'meɪtʃɪn/) che nel 1706 scopre (non sappiamo come) la formula
π/4=4 arctan(1/5)-arctan(1/239).
Utilizzando la serie di Gregory-Leibniz ora la convergenza è molto più rapida, e Machin riesce a calcolare π con ben 100 cifre decimali, e questo gli richiese il calcolo di una settantina di termini della serie relativa ad arctan(1/5) e di una quarantina di termini della serie relativa ad arctan(1/239). In suo onore, ogni espressione di π come somma o differenza di arcotangenti di frazioni viene chiamata Machin-like formula (in italiano potremmo tradurre con “formula di tipo Machin”). Possiamo dimostrare la formula di Machin utilizzando le formule di addizione e sottrazione per la tangente, oppure più elegantemente attraverso le identità complesse
(5+i)⁴=(24+10i)²=476+480i=2(1+i)(239+i),
da cui 4 arg(5+i)=arg(1+i)+arg(239+i) ovvero
4 arctan(1/5)= π/4+arctan(1/239).