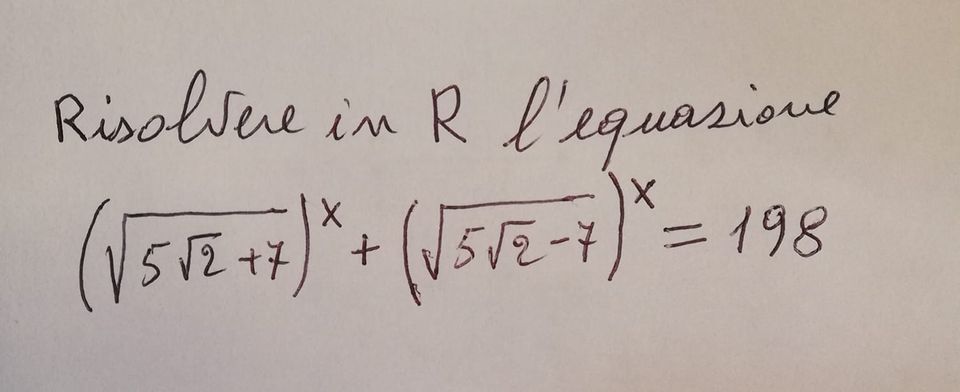
Scrivendo (√((5√2)-7))^x come 1/(√((5√2)+7))^x e procedendo per sostituzione otteniamo: y+(1/y)=198 da cui sviluppando: y^2-198x+1=0. È facile vedere che: le radici reali del polinomio di secondo grado sono x=4 e x=-4

Potrei:

u+v=198
u×v=1. t^2-198t+1=0

x=log(99+rad.quadrata di 9800)/log(radice quadrata di 5radicedi2-7)=-4
l'altra radice mi dà 4.

con i seguenti passaggi algebrici:

log(99+70radicequadrata di2)/log radice quadrata di 5radice di 2-7)=
2 log(radice quadrata di 99+70radice di 2 fratto 1/2 log(5radice di 2-7)=(radicali doppi)4log(5radice di 2-7) fratto log(5radice di 2-7)=4

con errata:

errata corrige:log(99-70radice quadrata di2)/log(radice quadrata di5radice di 2-7)

Poniamo una radice = A^(X/2) e l'altra = B^(X/2).

A^(X/2) × B^(X/2) = 1
quindi
A^(X/2) +B^(X/2) = 198 moltipl.tutto x A^(X/2)

A^(X/2) × A^(X/2) + 1 = 198 × A^(X/2)

Allora A^(X) = 198×A^(X/2) -1 e risolverla ma si nota che X deve essere 4 oppure 2^k
per esponente=8 vale la formula ma 198^4.

Un procedimento:

5√2-7 = [(5√2-7)(5√2+7)] / (5√2+7) = (50-49)/(5√2+7) = 1/(5√2-7).

Quindi, posto a = √(5√2+7), l'equazione originale è equivalente a:

aˣ + 1/aˣ = 198
a²ˣ - 198aˣ + 1 = 0
aˣ = 99±70√2 (entrambe soluzioni positive)
x·ln(a) = x·ln√(5√2+7) = ln(99±70√2)

Osservo ora che (5√2+7)² = 99 + 70√2 - non so motivare bene questo passaggio, ma è semplice da verificare. Inoltre, razionalizzazione in modo simile a sopra, 99±70√2 = 1/(99∓70√2) = (99+70√2)^(±1). Si conclude che:

(1/2)·x·ln(5√2+7) = ln[(5√2+7)^(±2)] = ±2·ln(5√2+7).

Semplificando, trovo x = ±4.

Ma la trasformazione da fare è la seguente:

99+70*2½ = 25*2+49±2*7*5*2½ = (5*2½ ± 7)²