Siano a, b, c tre interi positivi assegnati. Nel caso in cui l'equazione diofantea aX² + bY² = cZ²
sia possibile, determinare le soluzioni
Moltiplicando per a l'equazione
diventa X² + AY² = BZ²
Con A = a*b e B= a*c
Assumendo che {x, y, z} sia una soluzione e moltiplicando tutto per Bz^2 abbiamo
(BzZ)^2 = Bz^2X^2 + ABz^2Y^2 = (x^2 + Ay^2)X^2 + (Ax^2 + A^2y^2)Y^2 = (xX + AyY)^2 + A(yX -xY)^2
A(yX -xY)^2 = (BzZ)^2 - (xX + AyY)^2
Ovvero abbiamo una differenza di 2 quadrati esprimibile come la moltiplicazione
(BzZ - xX - AyY)(BzZ +xX + AyY) *
Ora con l'usuale procedura per le terne pitagoriche, si ricavano i valori delle incognite addizionando e sottraendo i termini del prodotto *
Quali espressioni ottieni per X, Y, Z?
a, b, c possono essere tre interi positivi arbitrari?
riscrivendo l'equazione nella forma
(X√a)²+(Y√b)²=(Z√c)² è poi lecito usare le relazioni sulle terne pitagoriche? Bisogna prima imporre che a,b,c siano quadrati perfetti?
Mi limito solo ad accennare una strada senza tuttavia percorrerla.
una soluzione non triviale esiste se e solo se
-a*b è residuo quadratico di c
a*c è residuo quadratico di b
c*b è residuo quadratico di a
E questo lo sappiamo per il teorema di Legendre. Stabilito il criterio di solvibilità, si procede come sopra per trovare una formula che dia le varie soluzioni, in dipendenza dai parametri
Conosciamo il teorema di Legendre. Il problema è, appunto, come hai detto e come richiede il quesito, trovare
X, Y, Z in funzione di parametri interi e della condizione di risolvibilità dell'equazione. Finché non si dispone di tali espressioni il problema non si può considerare risolto.
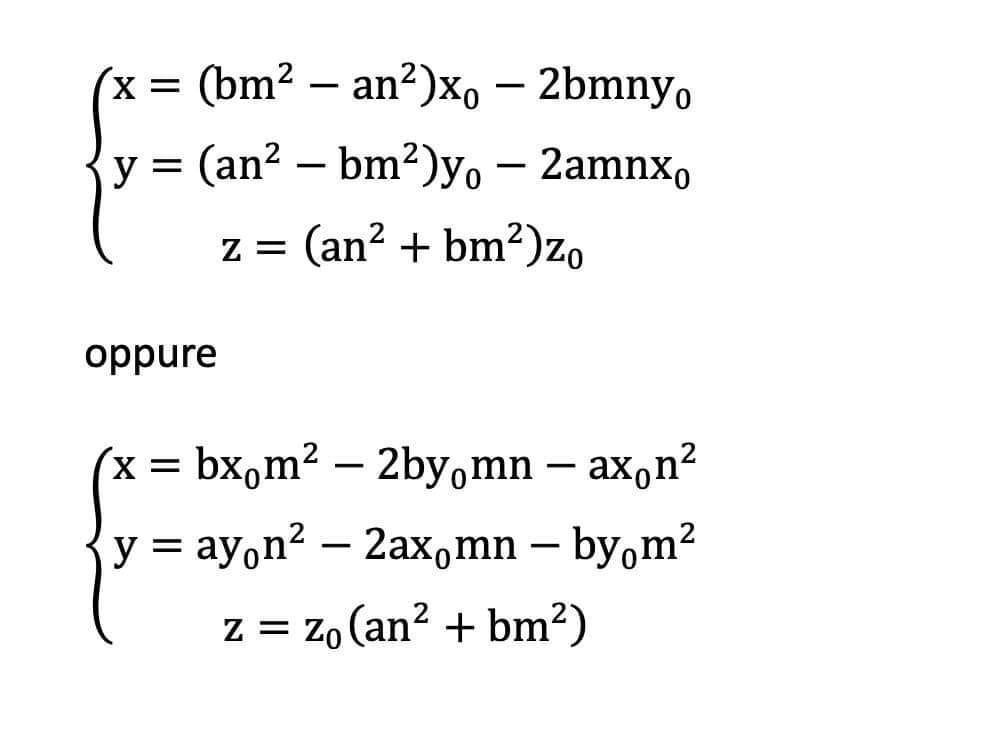
Sussiste il teo. per tale eq.ne detta di Legendre:
aX²+bY²=cZ² (1)
ha sol. non banali se:
- a, b, c ∈ ℕ privi di fattori quadrati e coprimi a due a due.
- ∃ k, h, m :
ak²+b=0 mod c
ch²-b=0 mod a
cm²-a=0 mod b
le soluzioni si ottengono risolvendo il sistema di congruenze quadratiche.
Un altro metodo è osservare che la superficie è una quadrica (ellisoide) razionale, quindi dividendo per Z²
con x=X/Z y=Y/Z
ax²+y²=c
nota una soluzione
intera x₀ y₀
possiamo intersecare la quadrica con la generica retta
x-x₀=λ(y-y₀)
e mettendo a sistema con la (2)
by²+2aλy+2ax₀-2aλy₀-c=0
da risolvere in y
imponendo Δ=R²
si puo cosí vedere se esiste una parametrizzazione
la condizione è che:
2ax₀+c=by₀²